고정 헤더 영역
상세 컨텐츠
본문

인지과학과 문제해결
prologue
Problem Space
Top-down VS Bottom-up
2018학년도 수학 영역 30번 (1)
2018학년도 수학 영역 30번 (2)
수학 공부와 문제해결
2018학년도 수학 영역 30번 (2)
암초를 만났을 때
멍- 해지거나, 여기까지 과정을 그냥 다시 되짚어보는 건 그다지 도움이 안 된다.
그보다는 어떤 부분에서 막혔는지 구체적으로 적어보고, 초심으로 돌아가 조건들을 다시 살펴보는 편이 좋다.
여기서 암초 상황을 적어보면
'k도 모르고, t도 몰라서 f(x)cos(πx)도 못 구하고 적분도 못한다.'
조건을 다시 보면 g(t)니까 t에 대한 함수이고 t가 변수
그리고 어떤 홀수 k는 구하는 값에 있으니 아직 몰라서 그렇지 정해진 값이다.
아, 이제 보니까 변하는 값은 t이고 k는 정해진 값인데 t를 고정시키고 k를 움직이고 있었구나?
t는 변수라서 어차피 다양한 값을 가진다.
그러니 k ~ k+8 미리 찍어놓고 t의 위치를 바꾸면서 보면,
어차피 정해지지 않을 것을 찾아다녔음을 알았게 된다.
이제 알 필요가 없어진 것으로 암초를 해결했다.
문제란 본래 내가 목표 상황에 도달해도 해결되지만, 목표 상황이 사라져도 해결되기 때문이다.
당장 f(x)로 할 게 사라졌으니 g(t)의 또 다른 축인 cos(πx)를 구하자.
순행 추리로 풀어갔으면 바로 이렇게 했을 거다.
f(x) 그렸으니 이번엔 cos(πx) 그려볼까!
코사인 그래프를 자주 그려봤으면 cos(πx)를 그리는 건 너무 쉽다.
x = 0일 때 cos(0) = 1
x = 1일 때 cos(π) = -1
x = 2일 때 cos(2π) = 1
그 사이는 가운데가 0임을 주의해서 예쁘게 곡선형으로 그려주고
이제 2 단위로 똑같이 그려주기만 하면 된다.
cos(πx)의 그래프도 그렸다.

그래프에 대해서 '수많은 값을 시각적으로 표시'라는 관점을 유지한다면
두 그래프를 겹쳐 그려서 곱의 값이 어떻게 되는지 관찰하는 건 자연스러운 과정이다.
그래서 f(x) 그리고 cos(πx)를 그리려고 했는데,
또 암초를 만났다.
이번 문제는 이렇다.
t가 변하는 값이라서 cos(πt)의 값을 알 수 없다. 그래서 그래프도 같이 못 그린다.

지금 상황은 조작자를 몰라서 상태를 못 바꾸는 상황은 아니다.
조작자를 '어디에' 적용해야할 지가 문제다.
암초를 잘 읽어보니, t가 변하는 값이라서 모른다고 했다.
아까 k는 정해진 값이라고 하지 않았나?
어차피 그려야할 부분은 x = k ~ k+8 구간이다.
그래서 cos(πk)를 생각해보기로 했다. 그런데 k라도 상황이 크게 다르지 않다고 생각하는 순간,
k가 홀수라는 사실과 cos(πx) 그래프에서 보이는 숫자의 규칙성이 떠오른다.
글만 봤으면 공감하기 어려울 수 있지만 직접 그려보면 바로 이해할 것이다.
k가 그래서 홀수였다. 미운 조건인줄 알았는데 이렇게 고마울 수가!
k가 어떤 값이어도 x = k ~ k+8에서 cos(πx)의 개형은 항상 같다는 사실을 알아냈다!

상당히 진도가 나간 것 같다.
이를 바탕으로 f(x)와 cos(πx)를 나란히 그려보자. 물론 곱하기 위해서.
t가 이정도 값이면 f(x)와 cos(πx)는 이렇게 그려지고

t가 이정도 값이면 f(x)와 cos(πx)는 이렇게 그려진다.

이제 박스 조건,
함수 g(t)가 t=α에서 극소이고 g(α)<0인 모든 α를 작은 수부터 크기순으로 나열한 것을 α1, α2, ···, αm (m은 자연수)라 할 때,

이다.
를 해석할 수 있다. 어떻게?
g(t)는 f(x)cos(πx)를 x = k ~ k+8에서 적분한 값이고
위의 그래프를 통해서 f(x)cos(πx)의 값을 대략 추정할 수 있다.
정확히 찍기는 어렵지만, 양수인지 음수인지와 가운데에서 곱의 크기가 가장 크다는 정도는 알 수 있다.
그 방식으로 대략 x = k ~ k+8에서 f(x)cos(πx) 그래프를 그리면
적분 값을 넓이로 해석해서(x축 위쪽은 양의 넓이, 아래쪽은 음의 넓이) g(t)를 대략 추정해서 해석하는 것이다.
참고로, 이때 극소를 보고 미분하여 =0인 값을 찾고 부호 변화를 관찰하여 극소를 찾는 조작자를 적용할 생각을 할 수도 있었다. 그러나 g(t)는 t에 대한 함수이므로 t에 대해 미분해야 하는데, 안타깝게도 미분을 하려면 적분을 직접 계산하고 미분해야하기 때문에 우선은 보류하는 편이 좋다고 판단했다.

다음과 같은 상황에서 g(t)는 0이다. 적분 구간 내에서 f(x)cos(πx)가 0이기 때문이다.

그러다가 이 순간을 경계로 (이때까지는 0이다)
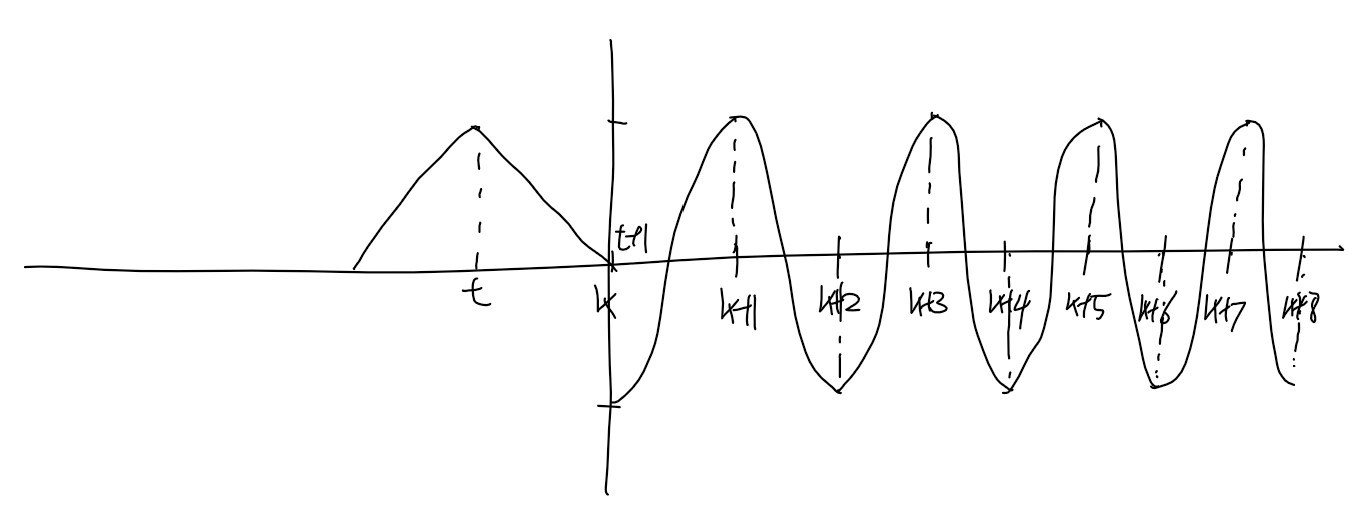
이렇게 되면 드디어 f(x)cos(πx)가 구간 내에서 음수로 들어가고 적분 값도 음수가 된다.

이 추세를 관찰하면 극소를 관찰할 수 있다.
..고 생각했다. 이 상황과

이 상황을 보니,

대략적인 추정에 한계가 왔음이 느껴진다. 그래도 보잘것없는 그림에 의존해서 조금 더 찍어보자.
첫 번째 그림은 그 다음 순간에 cos(πx)의 음의 부분과 곱해지는 영역을 보면 앞으로 더욱 강한 음의 값을 가질 것 같다.
cos(πx)의 양의 부분과 곱해지는 영역을 보면 앞으로 커지긴 하는데 음의 영역에 못 미칠 것 같다. 즉, 다음 값은 더 작을 것 같다는 말이다.
따라서 첫 번째 상황은 극소가 될 조건을 못 맞춘 것 같다.
두 번째 그림은 그 다음 순간에 cos(πx)의 음의 부분과 곱해지는 영역을 보면 고점을 지나서 음의 값이 약해지는 반면 cos(πx)의 양의 부분과 곱해지는 영역을 보면 앞으로 더 커지는 것 같다. 즉, 다음 값은 더 커질 것 같다는 말이다.
따라서 두 번째 상황은 극소가 될 조건을 갖춘 것 같다.
첫 번째 그림과 두 번째 그림 사이에 있었을 상태에 대한 추정은 이렇게 넘겼다.
첫 번째가 극소점이라면 어차피 같은 추정을 공유하는 두 번째까지 계속 증가할 것이고, 그 사이 상태들은 별 상관이 없다.
첫 번째가 극소점이 아니라면 두 번째 그림으로 가는 추정 중에서 가장 음의 값이 센 것이 바로 두 번째 그림이기 때문에 별 상관이 없다.
그런 식으로 f(x)를 옆으로 살살 밀면서 보면
(사실 가장 큰 점끼리 겹치는 곳에서 최대, 최소가 나오지 않을까싶은 감이다)
이 상황에선 느낌상 제일 큰 값을 가질 것 같고,

이 상황에선 제일 작은 값을 가질 것 같다.

극소점이라고 하면 그 근방에서 가장 작은 값이니
혹시 이런 지점(k, k+2, k+4, k+6, k+8)들이 전부 극솟값이 아닐까? 라는 의심이 든다.
가설을 만들었다.
구체화를 반복하다가 섣불리 일반화할 수는 없는 상태에서 가설을 세운 것이다.
가설을 그냥 참이라고 믿을 수는 없으니, 검증을 해보는 것이 옳은 순서다.
하지만 이 상황에선 검증을 하려면 식을 세워서 계산해보는 방법 밖에 없다.
이렇게 관찰하면서 구체화해봤으면 알겠지만, 경우를 상당히 많이 나눠야하고 그 경우에 대해서 일일이 다 적분을 해줘야 한다. 그렇게하기엔 계산량이 너무 많다.
그래서 우선 가설을 따라서 조건에 적용해보기로 한다.
가설을 따라 α들을 순서대로 나열하면 k, k+2, k+4, k+6, k+8이다.

에 따라 전부 더하면, 5k + 20 = 45
따라서 k = 5
공교롭게도, 어떤 홀수라는 조건에 잘 들어맞는다.
그리고 이를 적용하면
α값은 순서대로 5, 7, 9 ,11 ,13이다.

구하는 값에서 k =5 임은 밝혀졌다.
g(α)는 적분 값이다.
관찰하면서 α=5와 α=13에서 값의 분포가 같음을 보았으므로 적분 값도 같음을 알 수 있고
마찬가지로 α=7, 9, 11도 서로 적분 값이 같음을 알 수 있다.
그러니 각 경우에서 하나씩 계산하면 다른 값들을 계산하지 않아도 된다.
g(5)에서 다음 그래프를 보면 x = 5 ~ 6인 구간을 제외하고는 전부 0이므로
x = 5 ~ 6 구간에서만 적분하면 된다.
계산은 치환적분법, 부분적분법을 공부했으면 어렵지 않게 할 수 있다.
계산은 생략하고 g(5) = -2/π^2
g(7)도 같은 방식으로 계산하면
g(7) = -4/π^2
따라서

= 5 - (-2-4-4-4-2) = 21
최종적으로 가설 위에서 21이라는 값을 구했다.
틀릴 수도 있는데, 다행히 정답이 맞다.
그러나 이렇게 풀면 수학적으로 제대로 푼 것은 아니다.
가설이 참임을 검증하지 않았기 때문이다.
물론 가설을 검증하려면 계산을 해봐야한다.
이 글은 18학년도 수능 가형 30번에 대한 엄밀한 해설이 아니므로 생략한다.
여기까지 풀이를 따라왔다면 경우를 나눠서 g(t)를 직접 계산만 하면 됨을 알 수 있을 것이다.
그렇지만 경우가 많고 그 계산이 상당히 많기 때문에 생각보다 어려운 과정이라는 점을 알아둬야 한다. 수험생의 입장이라면 한번쯤 시도해볼만 하다.
'스터디플래닛 > 문제해결' 카테고리의 다른 글
| 인지과학과 문제해결: 수학 공부와 문제해결 (2) | 2019.05.11 |
|---|---|
| 인지과학과 문제해결: 2018학년도 수학 영역 30번 (1) (0) | 2019.05.11 |
| 인지과학과 문제해결: Top-down VS Bottom-up (0) | 2019.05.11 |
| 인지과학과 문제해결: Problem Space (0) | 2019.05.11 |
| 인지과학과 문제해결: prologue (0) | 2019.05.11 |
| 2018학년도 30번: 수학이라는 이름의 미궁 (0) | 2019.05.11 |





댓글 영역